우산정리

 

출처: https://blog.naver.com/artforlove/222017558685

 

 

 

오늘은 경시 기하의 기본이라고 할 수 있는 우산정리에 대해 알아보자.

 

우산정리를 사용할 수 있는 그림의 모양이 우산 모양과 비슷하다고 해서 이름이 우산정리이다.

하지만 다른 나라에서는 이 정리를 부르는 이름은 없다고 한다.

 

우산정리를 이용하는 경우는 세 가지밖에 없다.

간단히 말하자면 각각 각의 이등분선, 이등변삼각형, 수선과 지름이 있을 때 사용할 수 있다.

하지만 많은 문제에서 사용되기 때문에 반드시 알고 있어야 하는 정리이다.

 

1.각의 이등분선

 

지오지브라로 직접 그린 그림. 덕분에 오늘 처음으로 지오지브라를 써봤다.

 

---

NC × ND = NF × NE

---

pf)

∠CEN = ∠CDN = ∠FDN (∵호 NC에 대한 원주각)

∠CNE = ∠FND (∵조건)

∴△NCD∽△NFD (AA)

∴NC/NE = NF/ND 이므로(∵대응변)

NC × ND = NF × NE

■

 

 

2.이등변 삼각형

 

지오지브라로 직접 그린 그림222

 

---

QR²= QT²= QE₁ × QU (=QR × QT)

---

pf)

∠QRE₁ = ∠QUR (∵각각 호 QT, QR에 대한 원주각, QT = QR)

∠RQU는 공통

∴△QRE₁∽△QUR (AA)

∴QE₁/QR = QR/QU 이고(∵대응변)

QR = QT 이므로(∵조건)

QR²= QT²= QE₁ × QU (=QR × QT)

■

 

 

3.수선과 지름

 

지오지브라로 직접 그린 그림333

 

---

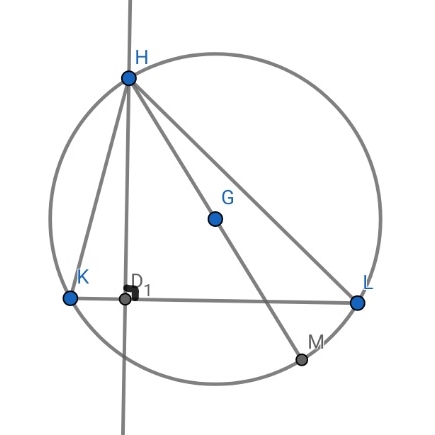
HK × HL= HD₁ × 2R

(R은 원의 반지름)

---

pf)

∠HD₁K = ∠HLM = 90˚ (∵HM이 원의 지름)

∠HKD₁ = ∠HML (∵호 HL에 대한 원주각)

∴△HKD₁∽△HML (AA)

∴HK/KD₁ = HM/HL 이고(∵대응변)

HM = 2R이므로

HK × HL= HD₁ × 2R

(R은 원의 반지름)

■

 

 

<참고>

 

지오지브라444

 

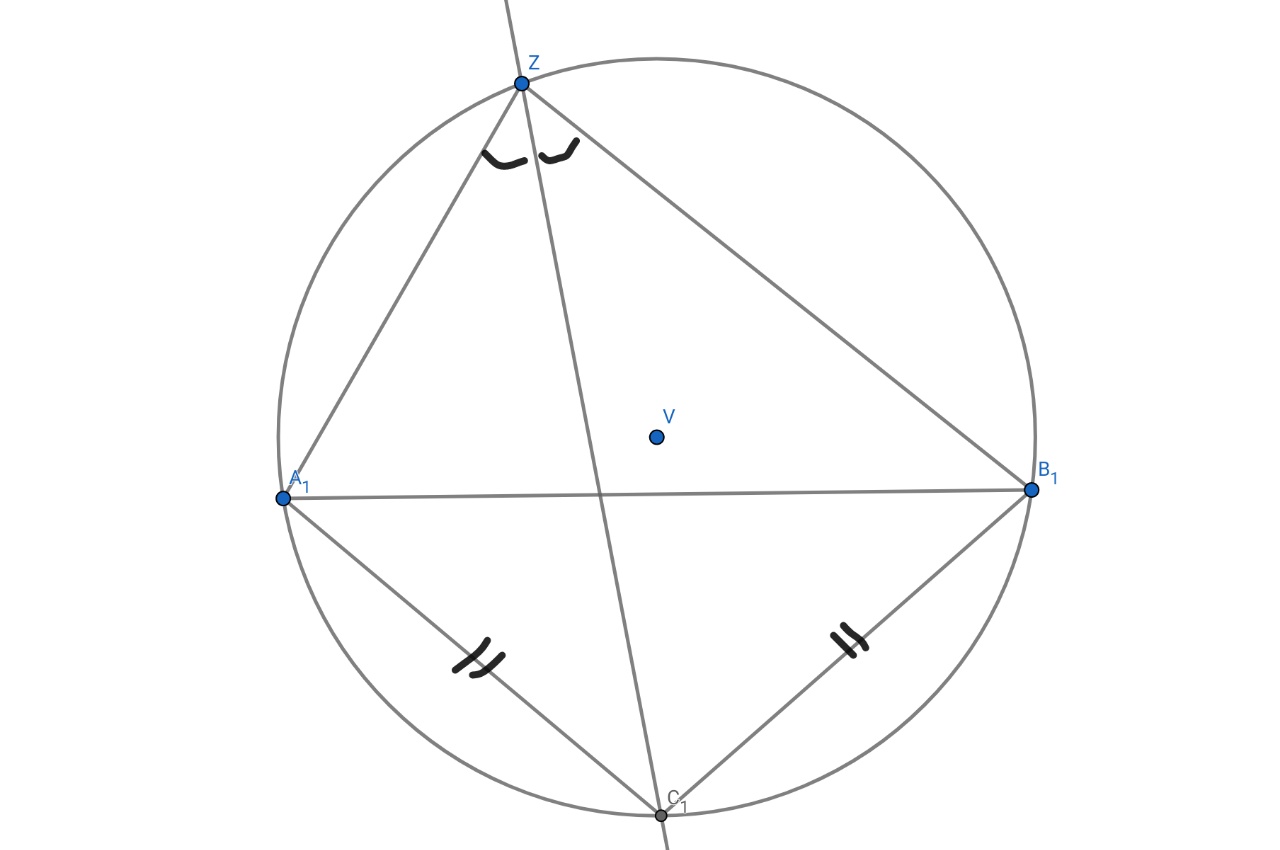
원주 위의 점들에 대해

각의 이등분선이 있으면 반대편에는 반드시 이등변삼각형이 있고,

이등변삼각형이 있으면 반대편에는 반드시 각의 이등분선이 있다.

(이는 원주각으로 자명하다.)

간단한 사실이지만 우산정리를 사용할 때 가끔 필요할 때가 있으니 알아두면 좋다.

 

 

 

 

오늘은 여기까지!

원래 우산정리를 이용한 간단한 예제들도 소개해 보려고 했지만 너무 길어져서 여기서 마치겠다.