2023. 9. 5. 11:10ㆍ대학수학 도전기

1. 푸리에 해석학의 기원
푸리에 해석학을 어쩌다가 고안하게 되었는지 나타내는 단원이다.
- 현의 진동 ( 진동하는 현은 1차원 파동 운동이다. 이를 간단히 2종류로 나눠 설명할 수 있다. )
1) 정상파
y=u(x, t) (x는 위치, t는 시각)
u(x, t)를 a(x)b(t)꼴로 나타낼 수 있는 경우다.
2) 진행파
u(x, t)=F(x-ct)인 경우다. ( c > 0 )
이 경우는 u(x, 0)이 좌표평면에서 오른쪽으로 이동한 것과 같다.
이제 파동 방정식을 유도해보자. 이는 악기의 음색을 담당하는 배음과 배음의 조합인 순음과 관련이 있다.
파동방정식

x축을 따라 x=0과 x=L 사이에 늘어진 균일한 하나의 현이 존재한다. 이 현이 진동하도록 놔두었을 때 y=u(x, t), 즉 y는 x와 t에 대한 함수다.
현을 위의 그림처럼 충분히 큰 수 N에 대해 x축을 따라 균일하게 분포하는 N개의 물체로 나눠 생각한다. 즉, 수직방향으로만 진동하는 N개의 입자로 구성된 계로 생각한다.
n번쨰 입자의 x좌표 xn=nL/N
yn=u(xn, t)라 두자. ( xn+1-xn=h, h=L/N )
현의 밀도 ρ > 0 가 일정하다고 가정 시, 각 입자의 질량은 ρh라 할 수 있다. 입자에 작용하는 중력을 ρhyn''(t)라 하자.
이 힘이 단순히 n-1번째, n+1번째 입자의 영향뿐이라고 가정하고 n번째 입자의 오른쪽에서 오는 힘은 1/h(yn+1-yn)에 비례한다고 가정 시, 장력을 다음과 같이 작성할 수 있다.
(τ/h)(yn+1-yn) τ > 0 은 장력 계수 값이다.
이를 기반으로 n-1번째 입자와 연관된 장력과 n+1번째 입자와 연관된 장력을 더해주고 변형한다. 과정은 다음과 같다.
ρhyn''(t)=(τ/h){yn+1(t)+yn-1(t)-2yn(t)}
yn의 표현식에서 트릭을 부려서 xn±a꼴로 대충 정리 (a는 h, -h, 0 )
h를 0으로 보내면 ρ∂2u/∂t2 = τ∂2u/∂x2 성립
이 때, c=√τ/ρ라 둔다면 다음과 같이 파동 방정식(1차원)이 나타난다.
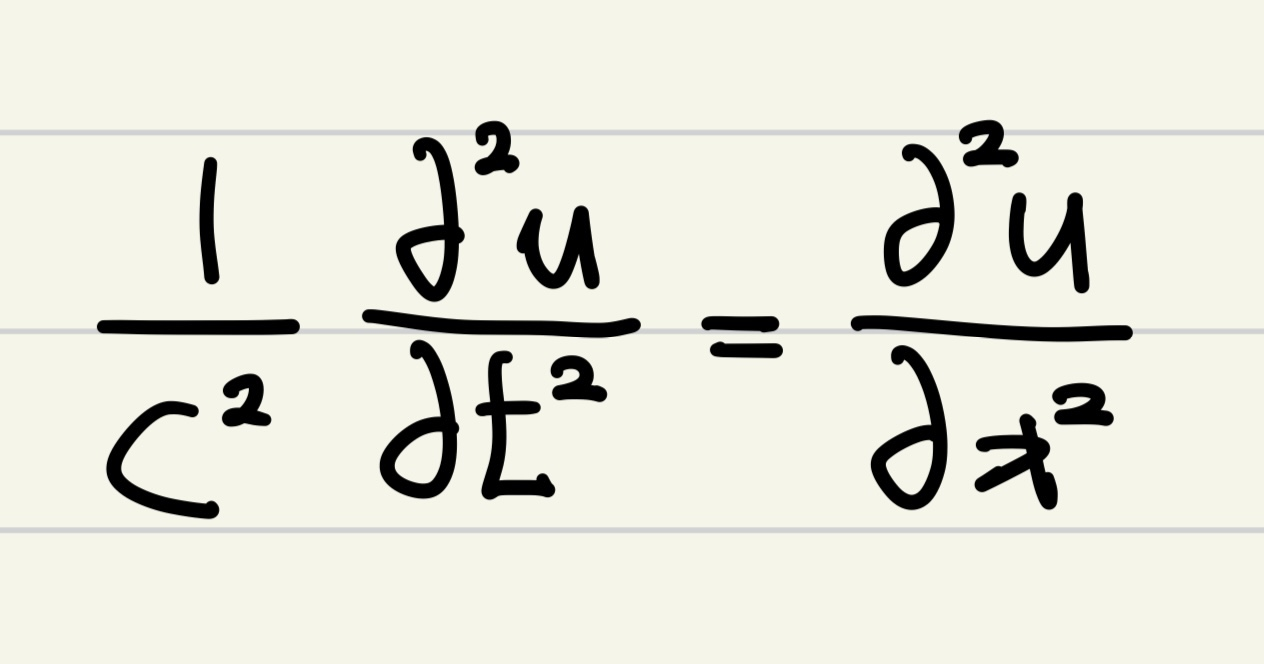
이제 이 방정식은 당연히 척도 변환(=단위 변환)이 가능하다. x=aX로 생각하고 X에 대한 식으로 재작성하는 과정이 척도 변환이다. 지금부터는 척도 변환을 통해 c=1로 단순화하고 L은 별도로 π로 두겠다.
즉, 다음을 풀도록 하겠다.

F가 임의의 두 번 미분가능한 함수일 때, F(x+t)와 F(x-t)는 파동 방정식의 해이다. ( 미분을 통해 확인 가능 )
이를 확장하여 반대 방향으로 이동하는 두 파동을 중첩하여 F, G가 두 번 미분가능한 함수라면 항상 u(x, t)=F(x+t)+G(x-t)가 파동방정식의 해임을 알 수 있고 모든 해가 저러한 꼴임을 보일 것이다.
m=x+t, n=x-t라 치환하고 v(m, n)=u(x, t)라고 하자.
∂2v/∂m∂n=0
이를 두 번 적분 시, v(m, n)=F(m)+G(n)을 얻는다. 즉, 적절한 F, G에 대해 u(x,t)=F(x+t)+G(x-t)로 나타낼 수 있다. 이제부터 이를 현의 물리적 운동과 관련지어 u(x, t)를 나타내는 달랑베르 공식을 유도해야 하는데 중간 과정에 적분기호도 좀 있고 그 뒤에 있는 열 방정식의 경우 이중적분이 등장하는 터라 일단 여기까지 하고 대책을 세워 돌아오도록 하겠다.
'대학수학 도전기' 카테고리의 다른 글
| 위상수학 개념 정리 1 미완 (1) | 2023.09.06 |
|---|---|
| 정수론 Kuldeep Singh 간단 정리 I (0) | 2023.09.03 |
| 현대대수학 개념 정리 2 (0) | 2023.09.01 |
| 현대대수학 개념 정리 1 (0) | 2023.09.01 |
| 선형대수학 공부하기 1일차 (0) | 2023.06.28 |